# ELLIPTIC CURVES IN CRYPTOGRAPHY # Đường cong elliptic Đường cong Elliptic là một đường cong trong hình học đại số, được xác định bởi phương trình đại số có dạng: y^2 = x^3 + ax + b Với a, b là các hằng số số thực và `4a^3 + 27b^2 # 0`. Phương trình trên được gọi là dạng chuẩn Weierstrass cho các đường cong elip. Đường cong này có điểm đặc biệt gọi là điểm "vô cùng" và được ký hiệu là O. Đường cong Elliptic có những tính chất đặc biệt, chẳng hạn như nó là một đường cong mượt (smooth curve), tức là không có đỉnh, cusp hoặc self-intersection points. Điều này cho phép nó được sử dụng trong nhiều lĩnh vực, từ mã hóa đến lý thuyết số và hình học. Một trong những tính chất quan trọng nhất của đường cong Elliptic là nó có một phép toán "cộng" trên các điểm trên đường cong, được gọi là phép toán toán học trên đường cong Elliptic. Phép toán này cung cấp cho đường cong Elliptic một cấu trúc nhóm đặc biệt, cho phép nó được sử dụng trong các ứng dụng mã hóa và xác thực bảo mật. (Sẽ được phân tích kĩ hơn ở bên dưới) 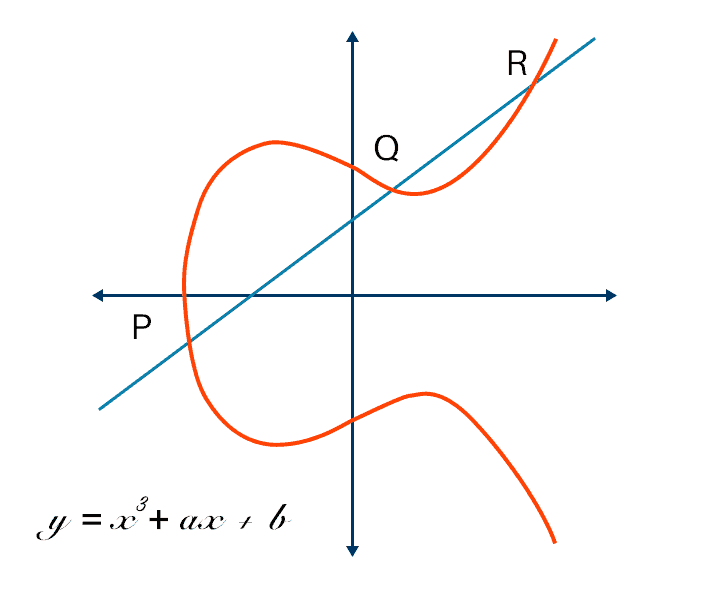 ## Phép cộng 2 điểm trên đường cong Elliptic 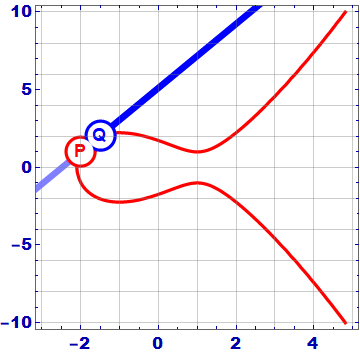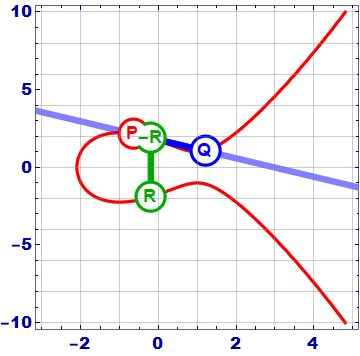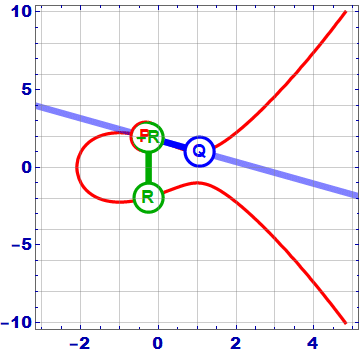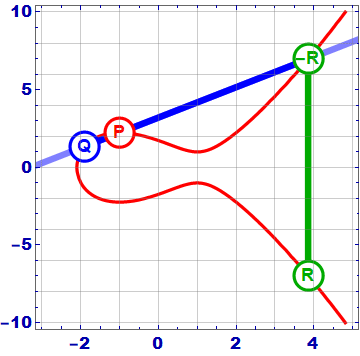 Trên phương diện hình học, phép cộng 2 điểm P và Q theo biểu thức P + Q = R trên đường cong Elliptic được thực hiện như sau: Qui ước: - Điểm O là phần tử đơn vị của phép cộng. Như vậy với P∈ E(a,b), P ≠ 0 thì P + 0 = 0+P=P - Phần tử nghịch đảo của điểm P trong phép cộng, ký hiệu – P, là điểm đối xứng với P qua trục hoành Kẻ đường thẳng d đi qua 2 điểm P và Q, đường thẳng sẽ cắt đường cong Elliptic tại điểm thứ 3 là -R. Phần tử nghịch đảo của -R là R chính là kết quả của phép cộng hai điểm P và Q trong đường cong Elliptic. Nếu P và Q trùng nhau thì đường thẳng d chính là tiếp tuyến của đường cong tại điểm P và thực hiện tương tự như trên. Trên phương diện số học, các bước thực hiện sẽ có chút phức tạp hơn - Nếu P = Q: - Tính đạo hàm của đường cong tại P: m = (3x_p^2 + a) / (2y_p) - Tính tọa độ của R: x_R = m^2 - 2x_p, y_R = m(x_p - x_R) - y_p - Nếu P ≠ Q: - Tính độ dốc của đường thẳng đi qua P và Q: m = (y_q - y_p) / (x_q - x_p) - Tính tọa độ của R: x_R = m^2 - x_p - x_q, y_R = m(x_p - x_R) - y_p Trong trường hợp P và Q đối xứng qua trục hoành, hay nói cách khác Q = -P thì đường thẳng nối P, Q sẽ cắt đường cong Elliptic tại vô cực, hay P + ( -P ) = 0 Các phép tính này có thể được áp dụng cho đường cong Elliptic trên một trường hữu hạn, nơi các toán tử cộng, trừ, nhân và chia được định nghĩa trên các phần tử của trường hữu hạn đó. Các tính chất của đường cong Elliptic đã làm cho nó trở thành một công cụ hữu ích trong các ứng dụng mã hóa và xác thực bảo mật. ## Phép nhân vô hướng trên đường cong Elliptic (**Scalar multiplication**) Ngoài phép cộng, chúng ta có thể định nghĩa một phép toán khác: phép nhân vô hướng, nghĩa là: ```jsx nP = P + P + P +...+ P (n time) ``` Đk: `n`là số tự nhiên Như vậy để thực hiện phép nhân vô hướng nP, ta phải cộng n lần các điểm P lại với nhau. Nếu n có k bit nhị phân thì độ phức tạp của phép toán sẽ là O(2^k), điều này không thực sự tốt. Nhưng ta có thể thực hiện một số phép toán tối ưu hơn với độ phức tạp giảm đáng kể như sau. Một trong số đó là thuật toán **double and add.** Nguyên tắc hoạt động của nó có thể được giải thích rõ hơn với một ví dụ: Chọn n = 151, dạng nhị phân của n như sau: 10010111. Biểu diễn nhị phân này có thể được chuyển thành tổng lũy thừa của hai: $151 = 2^7 + 2^4 + 2^2 + 2^1 + 2^0$ Theo cách thức này, ta có thể nhân P vào cả 2 vế, được biểu thức như sau: $151P = 2^7P + 2^4P + 2^2P + 2^1P + 2^0P$ Cuối cùng, thuật toán **double and add** được mô tả như sau: ``` Input: P in E and an integer n > 0 1. Set Q = P and R = O. 2. Loop while n > 0. 3. If n ≡ 1 mod 2, set R = R + Q. 4. Set Q = 2 Q and n = ⌊n/2⌋. 5. If n > 0, continue with loop at Step 2. 6. Return the point R, which equals nP. ``` # Đường cong Elliptic trong trường hữu hạn(Fp) và ứng dụng trong mật mã Bây giờ chúng ta sẽ giới hạn các đường cong elliptic của mình trong các trường hữu hạn, thay vì tập hợp các số thực và xem mọi thứ thay đổi như thế nào. ## Đường cong Elliptic trong trường hữu hạn(Fp) Đường cong elliptic trong trường hữu hạn Fp là một loại đường cong elliptic mà tất cả các điểm trên đường cong được định nghĩa trong một trường hữu hạn Fp, trong đó p là một số nguyên tố. Các điểm trên đường cong elliptic Fp được biểu diễn bởi các cặp số nguyên (x,y), trong đó x và y đều là các phần tử của trường hữu hạn Fp, và thỏa mãn phương trình đường cong elliptic: y^2 = x^3 + ax + b ⇒ y^2 = x^3 + ax + b (mod p) trong đó a và b là các hệ số trong trường hữu hạn Fp và thỏa mãn điều kiện 4a^3 + 27b^2 ≠ 0 để đảm bảo rằng đường cong không phải là một đường thẳng. Một trong những ứng dụng quan trọng của đường cong elliptic trong trường hữu hạn Fp là trong mật mã học. Cụ thể, phép toán trên điểm của đường cong elliptic Fp có tính chất khó tính ngược lại, tạo ra một cơ chế bảo mật mạnh để sử dụng trong các giao thức mật mã học như mã hóa khóa công khai và chữ ký số. 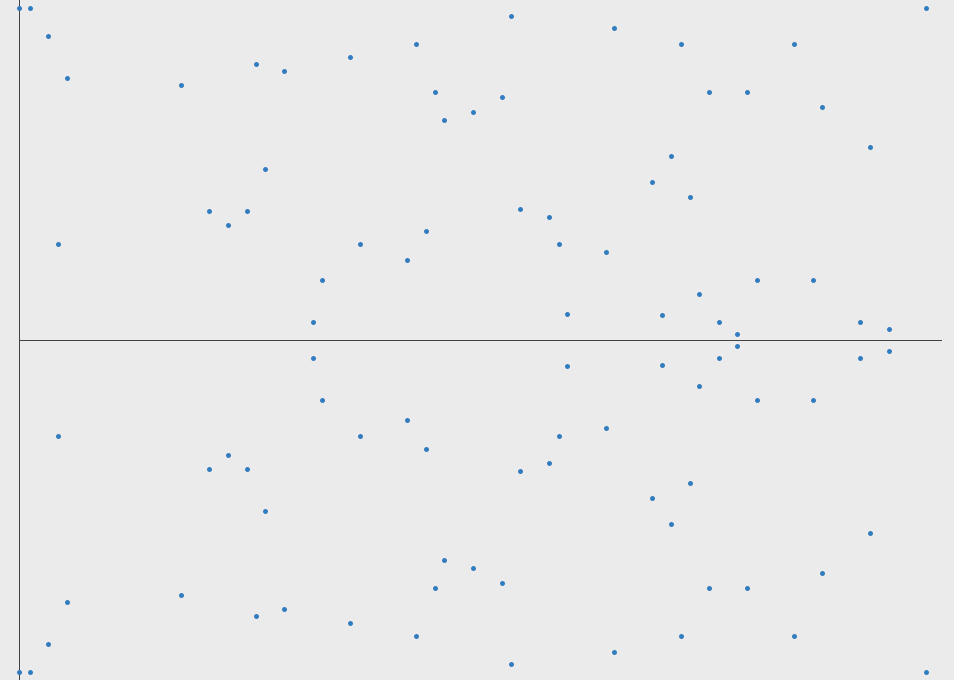 Những gì trước đây là một đường cong liên tục bây giờ là một tập hợp các điểm rời rạc trong hệ tọa độ xy. Và ta có thể thấy sự đối xứng giữa các điểm. ## Luật nhóm của đường cong Elliptic trong trường hữu hạn Fp Đường cong Elliptic trên trường hữu hạn Fp là một nhóm Abelian vì nó thỏa mãn cả hai tính chất của nhóm và tính chất của nhóm Abelian. Cụ thể, như đã biết, đường cong Elliptic thỏa mãn các tính chất của nhóm bao gồm tính kết hợp, phần tử đơn vị, phần tử nghịch đảo và tính giao hoán. Trong khi đó, tính chất của nhóm Abelian là tính giao hoán và phép cộng là phép toán có tính chất giao hoán. Nghĩa là, phép cộng hai phần tử bất kỳ trên đường cong Elliptic có tính chất giao hoán. Điều này có nghĩa là phép cộng P + Q sẽ tương đương với phép cộng Q + P. Vì vậy, đường cong Elliptic trên trường hữu hạn Fp thỏa mãn cả tính chất của nhóm và tính chất của nhóm Abelian, do đó được gọi là một nhóm Abelian. ## Phép cộng 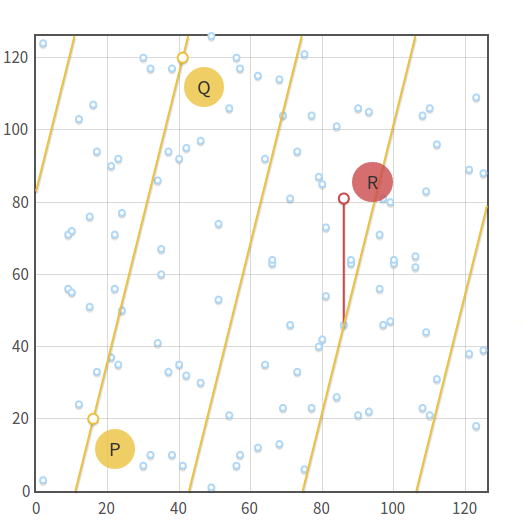 $E : y^2 = x^3 - x + 3 (mod 127), P(16, 20) , Q (41, 120),P+Q=R$ Phép cộng hai điểm trên đường cong Elliptic trong trường hữu hạn Fp được thực hiện bằng cách sử dụng công thức cộng của đường cong Elliptic. Cho hai điểm P và Q trên đường cong Elliptic, ta cần tính toán tổng P + Q bằng cách sử dụng các tham số của đường cong Elliptic và phép toán trên trường hữu hạn Fp. Cụ thể, công thức để tính toán P + Q là: - Nếu P = O (phần tử đơn vị), tổng P + Q sẽ là Q. - Nếu Q = O (phần tử đơn vị), tổng P + Q sẽ là P. - Nếu P = -Q (nghĩa là hai điểm trên đường cong đối xứng qua trục hoành), tổng P + Q sẽ là phần tử đơn vị O. - Nếu P ≠ Q, công thức cộng sẽ là: - Tính độ dốc của đường thẳng đi qua P và Q (lưu ý, nếu P và Q trùng nhau thì đường thẳng này là tiếp tuyến của đường cong tại P). - Tìm điểm giao của đường thẳng và đường cong Elliptic. Điểm này sẽ được ký hiệu là R. - Điểm R sẽ được phản xạ qua trục hoành để tính toán kết quả P + Q. Công thức chi tiết để tính toán điểm phản xạ R qua trục hoành là: x_R = s^2 - x_P - x_Q y_R = -y_P + s * (x_P - x_R) trong đó: s = (y_P - y_Q) / (x_P - x_Q) Nếu P = Q, công thức cộng sẽ được thay thế bằng công thức nhân (tính đạo hàm tại điểm P và sử dụng phép cộng trên trường hữu hạn). Việc tính toán phép cộng trên đường cong Elliptic trong trường hữu hạn Fp rất quan trọng trong các ứng dụng mã hóa và bảo mật thông tin. ```python def add_point(p1, p2): if p1 == (0, 0): return p2 if p2 == (0,0): return p1 x1, y1 = p1 x2, y2 = p2 if x1 == x2 and y1 == -y2: return (0, 0) lamda = 0 if p1 == p2: lamda = ((3*pow(x1,2,p)+a) * inverse(2*y1, p)) else: lamda = ((y2-y1) * inverse(x2-x1, p)) x3 = (pow(lamda, 2) - x1 - x2) % p y3 = (lamda*(x1 - x3) - y1) % p return (x3, y3) ``` ## Phép nhân vô hướng Chúng ta sẽ sử dụng thuật toán **double and add** tương tự như đường cong Elliptic trong trường số thực kết hợp thêm phép (mod p) để đảm bảo kết quả sẽ là một điểm ở trong trường hữu hạn Fp. Phép nhân vô hướng nP với P là một điểm trên đường cong Elliptic trong trường hữu hạn Fp là phép tính nhân một điểm trên đường cong Elliptic với một số nguyên dương n. Công thức tính toán phép nhân vô hướng là: ``` Input: P in E(Fp) and an integer n > 0 1. Set Q = P and R = O. 2. Loop while n > 0. 3. If n ≡ 1 mod 2, set R = R + Q. 4. Set Q = 2 Q and n = ⌊n/2⌋. 5. If n > 0, continue with loop at Step 2. 6. Return the point R, which equals nP. ``` Việc tính toán phép nhân vô hướng này có thể được tối ưu bằng cách sử dụng các thuật toán như Montgomery ladder hay double-and-add. Các thuật toán này giúp giảm số lần tính toán trên đường cong Elliptic và tăng tốc độ tính toán. Việc tính toán phép nhân vô hướng trên đường cong Elliptic trong trường hữu hạn Fp cũng rất quan trọng trong các ứng dụng mã hóa và bảo mật thông tin. $VD: E: y^2 = x^3 + 2x + 3(mod 97), P (3,6)$ 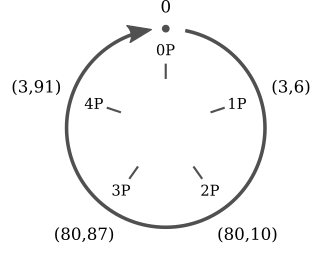 ```python def Scalar_Mul(P, n): Q = P R = (0, 0) while n > 0:

If n ≡ 1 mod 2, set R = R + Q. if n % 2 == 1: R = add_point(R, Q)

Set Q = 2 Q and n = ⌊n/2⌋. Q = add_point(Q, Q) n = n//2 return R ``` ## Order của đường cong Elliptic trong trường Fp Trong lý thuyết đường cong elliptic, "order" của một đường cong elliptic được định nghĩa là số lượng điểm trên đường cong đó, bao gồm cả điểm vô cùng. Trong trường hợp đường cong elliptic được xác định trên trường hữu hạn Fp (trong đó p là số nguyên tố), thì "order" của nó được ký hiệu là |E(Fp)|. Việc tính toán "order" của một đường cong elliptic trên trường hữu hạn Fp có thể trở nên rất phức tạp, và cần sử dụng các thuật toán đặc biệt để giải quyết vấn đề này. Một trong những phương pháp tính toán "order" của một đường cong elliptic là thuật toán [Schoof](https://en.wikipedia.org/wiki/Schoof%27s_algorithm). Tuy nhiên, nếu đường cong elliptic được xác định trên trường Fp và có thể được viết dưới dạng y^2 = x^3 + ax + b (mod p) (với a, b là các số nguyên trong trường Fp), thì theo định lý Hasse, ta có thể xác định được giới hạn trên và dưới cho "order" của đường cong elliptic đó như sau: p + 1 - 2*sqrt(p) ≤ |E(Fp)| ≤ p + 1 + 2*sqrt(p) Với cách tính này, ta có thể ước tính được "order" của đường cong elliptic một cách đáng tin cậy. ## Subgroup Order Trong đường cong elliptic trên trường hữu hạn Fp, Subgroup order (bậc nhóm con) là bậc của một nhóm con của các điểm trên đường cong. Một nhóm con là một tập con của các điểm trên đường cong mà khi được thực hiện phép toán nhân với một số nguyên dương nào đó, kết quả vẫn thuộc tập hợp đó. Cụ thể, cho một điểm P trên đường cong và một số nguyên dương n, ta có thể tạo ra một nhóm con bằng cách lấy tất cả các điểm Q trên đường cong sao cho Q = n * P. Bậc nhóm con của điểm P là số lượng các điểm trên đường cong trong nhóm con này. Theo định lý Lagrange, bậc nhóm con của một điểm trên đường cong là một ước số của bậc của đường cong. Vì vậy, nếu bậc của đường cong là một số nguyên tố, thì bậc nhóm con của mỗi điểm trên đường cong sẽ là 1, p hoặc một ước số của p. Điều này là cơ sở cho việc sử dụng đường cong elliptic trong ECC, vì nếu một điểm P trên đường cong có bậc nhóm con bằng p thì P có thể được sử dụng như một Base Point để tạo ra các khóa bảo mật trong hệ thống ECC. ## **Finding a base point** Trong đường cong elliptic trên trường hữu hạn Fp, một base point (điểm cơ sở) là một điểm P trên đường cong, được sử dụng để tạo ra các khóa bảo mật trong hệ thống ECC. Một base point thường được chọn với các thuộc tính sau: 1. Nó thuộc về đường cong elliptic trên trường hữu hạn Fp. 2. Nó có thứ tự lớn, tức là bậc của P (số lượng điểm trên đường cong được tạo ra bằng cách lặp điểm P) là một số lớn. 3. Không có một số nguyên dương k nào mà kP bằng điểm vô cực trên đường cong elliptic. Tìm một base point trong đường cong elliptic trên trường hữu hạn Fp thường được thực hiện bằng phương pháp thử và sai. Tức là, ta chọn một điểm bất kỳ trên đường cong, tính toán bậc của điểm đó, và kiểm tra xem nó có đủ lớn để sử dụng làm base point hay không. Nếu điểm này không phải là base point, ta chọn một điểm khác và tiếp tục thử và sai. Một cách khác để tìm base point là sử dụng các giải thuật tìm kiếm cục bộ như phương pháp Pollard's rho hoặc phương pháp kangaroo. Tuy nhiên, các phương pháp này thường chỉ cho kết quả tốt khi bậc của đường cong elliptic không quá lớn. Việc chọn một base point phù hợp là rất quan trọng trong hệ thống ECC, vì nó ảnh hưởng đến tính an toàn và hiệu suất của hệ thống. ## **Discrete logarithm** Trong đường cong elliptic trên trường hữu hạn Fp, logarit rời rạc (discrete logarithm) là việc tìm một số nguyên dương k sao cho khi nhân một điểm P trên đường cong với k, ta thu được một điểm Q trên đường cong, tức là Q = kP. Logarit rời rạc là một vấn đề quan trọng trong ECC, vì nó liên quan đến tính toán các khóa bảo mật trong hệ thống ECC. Tuy nhiên, việc tìm logarit rời rạc trong đường cong elliptic là một vấn đề khó khăn và chưa có giải pháp hiệu quả nhất định cho việc giải quyết nó. Tuy nhiên, có một số phương pháp được sử dụng để xấp xỉ logarit rời rạc, bao gồm: 1. Phương pháp Babystep-Giantstep: Phương pháp này sử dụng kỹ thuật tìm kiếm liên tục để tìm logarit rời rạc. Nói chung, phương pháp này có độ phức tạp O(sqrt(n)), n là bậc của đường cong elliptic. 2. Phương pháp Pollard's Rho: Phương pháp này cũng sử dụng kỹ thuật tìm kiếm liên tục để tìm logarit rời rạc. Độ phức tạp của phương pháp này phụ thuộc vào việc lựa chọn hàm băm. 3. Phương pháp Pohlig-Hellman: Phương pháp này sử dụng việc phân tích thành thừa số nguyên tố để tìm logarit rời rạc. Độ phức tạp của phương pháp này phụ thuộc vào các ước số nguyên tố của bậc của đường cong. Các phương pháp này được sử dụng để xấp xỉ giá trị của logarit rời rạc trong đường cong elliptic trên trường hữu hạn Fp, và chúng có thể được áp dụng để giải quyết các vấn đề liên quan đến tính toán khóa bảo mật trong ECC. ## Ứng dụng của đường cong Elliptic trong mật mã học 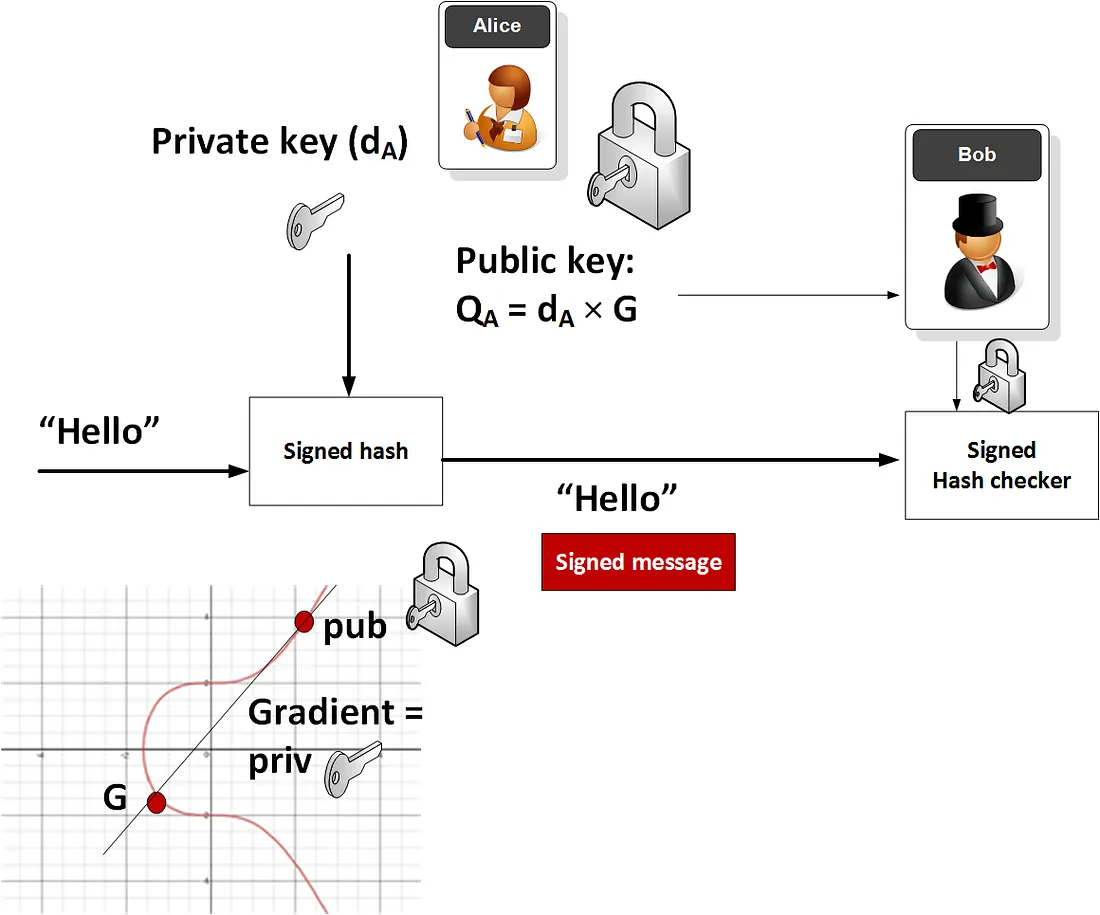 ### ****Digital Signatures and Key Exchange**** Hai ứng dụng chính của ECC là chữ ký số (****Digital Signatures****) và trao đổi khóa (****Key Exchange****). Trong quá trình trao đổi khóa, chúng ta có thể sử dụng một phương pháp tương tự như phương pháp Diffie-Hellman thường thấy: ECDH. Với điều này, cả Bob và Alice đều tạo ra các cặp khóa của riêng mình và sau đó trao đổi các giá trị khóa công khai với người còn lại. Tiếp theo, nhân khóa công khai được chia sẻ với các khóa riêng của chính mình và kết quả sẽ là Khóa trao đổi (Shared Key)-là 1 điểm trên đường cong Elliptic. Giá trị x_hoành độ của điểm thường được sử dụng làm giá trị được chia sẻ và giá trị này có thể được sử dụng để tạo khóa mã hóa 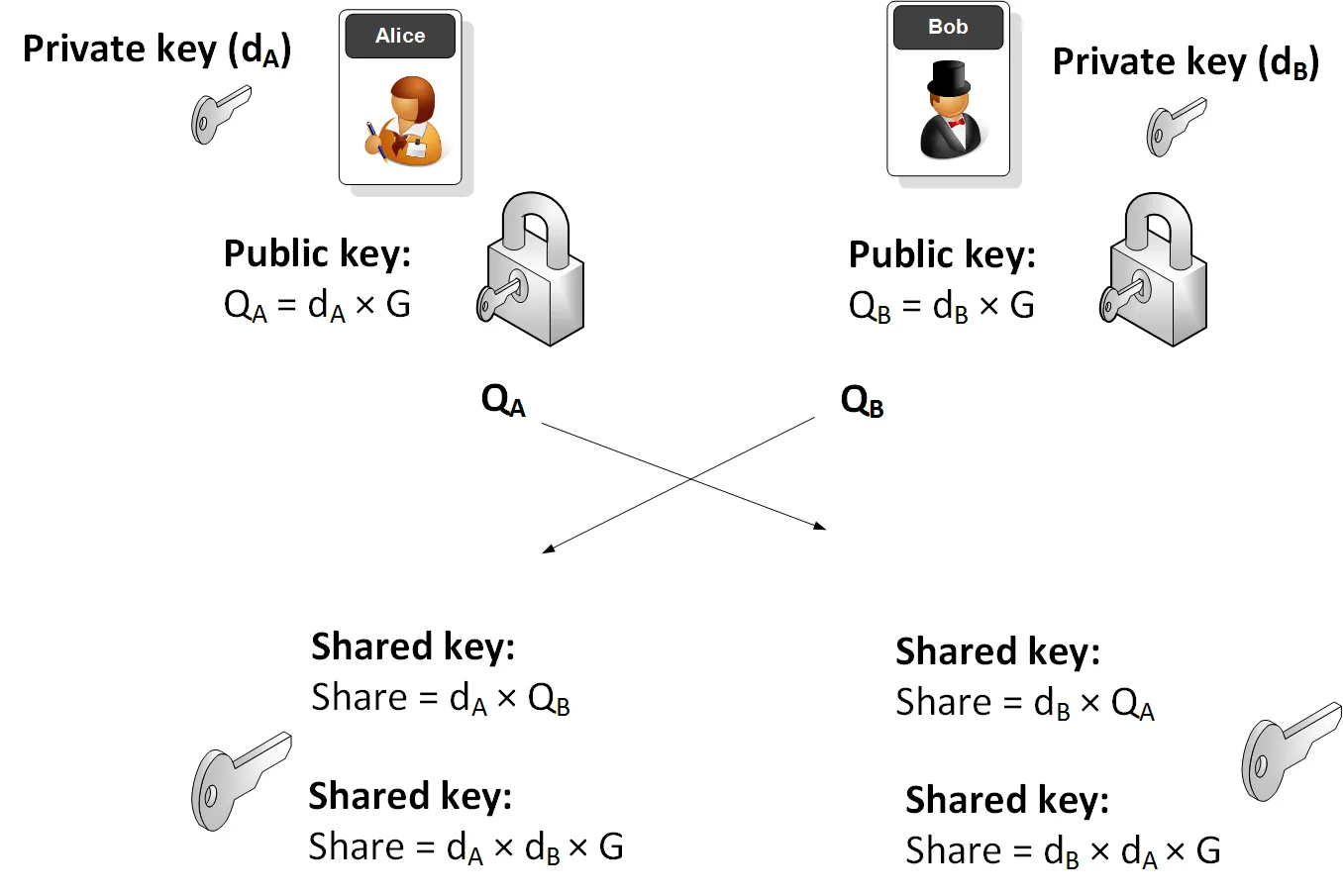 VD: [https://asecuritysite.com/encryption/ecdh2](https://asecuritysite.com/encryption/ecdh2) ```python G: (55066263022277343669578718895168534326250603453777594175500187360389116729240L, 32670510020758816978083085130507043184471273380659243275938904335757337482424L) P: 115792089237316195423570985008687907853269984665640564039457584007908834671663 Alice's secret key: 11302873530277286977317330088775295887228613968519091334644437952622729383175 Alice's public key: (43762022694931184757492607356752180905518342017728551120282167112666275442351L, 114384988717018399469597034834957578408750274128921832447140766594105794755401L) Bob's secret key: 57357023452856094330375933847127925090028363431260832480927591194583881325524 Bob's public key: (55091946369527979001134485845266995342724549818123857460791054009076326226426L, 97187020471842083008659802753584322405090644904628617139758459912605661136781L) ========================== ========================== Alice's shared key: (57532214745918139757345382685094974834256492408547750418623750043147069440196L, 96501482835335029014756728397878054304682795886955595404840493797142776000789L) Bob's shared key: (57532214745918139757345382685094974834256492408547750418623750043147069440196L, 96501482835335029014756728397878054304682795886955595404840493797142776000789L) ========================== The shared value is the x-value: 57532214745918139757345382685094974834256492408547750418623750043147069440196 ``` Một ứng dụng khác của ECC là chữ ký số, chẳng hạn như đối với Thuật toán chữ ký số Elliptic Curve . Với điều này, Alice sẽ tạo một cặp khóa, hash tin nhắn bằng khóa riêng của cô ấy. Sau đó, cô ấy gửi tin nhắn và hàm băm đã ký cho Bob, người này sẽ lấy hàm băm của chính anh ấy trong tin nhắn và giải mã phiên bản băm của Alice bằng khóa công khai của cô ấy. Nếu giá trị băm khớp, anh ta đã chứng minh rằng Alice đã gửi tin nhắn và tin nhắn đó không thay đổi: 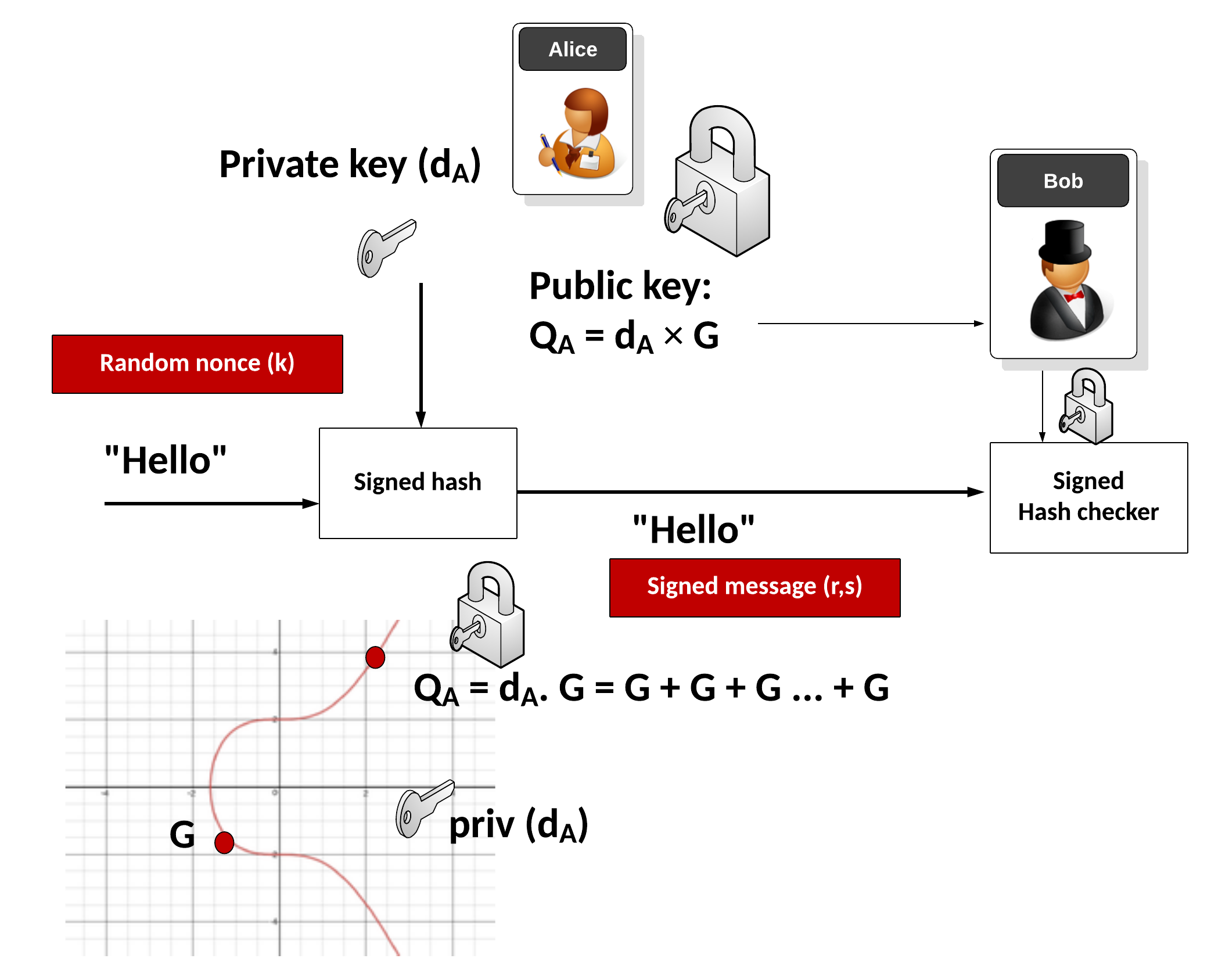 [https://asecuritysite.com/encryption/ecdsa2](https://asecuritysite.com/encryption/ecdsa2) Các bước khởi tạo chữ ký số trong thuật toán ECDSA bao gồm: 1. Tạo ra cặp khóa công khai và khóa bí mật cho người dùng: Để thực hiện điều này, ta cần tạo ra một đường cong elliptic và một điểm gốc trên đường cong. Sau đó, sử dụng thuật toán Diffie-Hellman, ta tính được khóa công khai và khóa bí mật cho người dùng. 2. Tạo ra thông điệp cần ký: Đây là thông tin cần được ký và gửi đi. 3. Tính toán giá trị băm của thông điệp: Sử dụng một hàm băm như SHA-256 hoặc SHA-512, ta tính toán được giá trị băm của thông điệp cần ký. 4. Tạo chữ ký số: Đầu tiên, ta tạo một số ngẫu nhiên gọi là `k`. Sau đó, tính toán đường cong elliptic `P = k * G`, trong đó G là base point trên đường cong. Tiếp theo, tính toán giá trị `r = xP (mod n),` trong đó `xP` là hoành độ của điểm P trên đường cong elliptic và n là order của base point G. Sau đó, tính toán giá trị `s = k^(-1) * (hash + d*r) (mod n)`, trong đó `d` là khóa bí mật của người ký và hash là giá trị băm của thông điệp cần ký. Cuối cùng, chữ ký số là cặp giá trị `(r,s).` 5. Gửi thông điệp và chữ ký số đến người nhận. Sau khi nhận được thông điệp và chữ ký số, người nhận sẽ thực hiện quá trình xác thực để kiểm tra tính hợp lệ của chữ ký số. Quá trình xác nhận (verification) chữ ký số trong ECDSA bao gồm các bước sau: 1. Nhận được thông điệp gốc M, chữ ký số `(r,s)` và khóa công khai của người ký ECDSA (Q). 2. Tính băm SHA-1 hoặc SHA-256 của thông điệp gốc M, đây là giá trị h. 3. Tính `w = s^-1 mod n`, với n là order của base point G trên đường cong elliptic, tương ứng với khóa cá nhân của người ký ECDSA. 4. Tính `u1 = hash.w mod n` và `u2 = r.w mod n.` 5. Tính điểm `W = u1*G + u2*Q` trên đường cong elliptic. Nếu W = O (điểm vô cùng), thì chữ ký số không hợp lệ. 6. Tính `r' = x(W) mod n`. Nếu r' khác với giá trị r được gửi kèm theo thì chữ ký số không hợp lệ. 7. Nếu `r'` bằng với giá trị `r` được gửi kèm theo, thì chữ ký số là hợp lệ. Ngược lại, nếu `r'` khác với `r` thì chữ ký số không hợp lệ. Quá trình xác nhận chữ ký số trong ECDSA sẽ giúp cho người nhận thông điệp có thể đảm bảo rằng thông điệp đó được gửi từ người ký đã được xác thực và không bị sửa đổi trên đường truyền.